Лекции
1
Лекция 1. Классическая дифференциальная геометрия. Введение
01:34:05
2
Лекция 2. Кривые в трехмерной области
01:29:44
3
Лекция 3. Поверхности
01:12:48
4
Лекция 4. Перепараметризация поверхностей
01:10:24
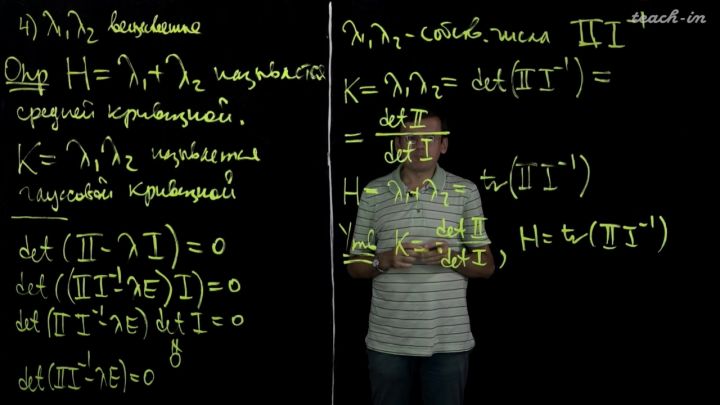
5
Лекция 5. Кривизна поверхности
01:00:49
6
Лекция 6. Современный взгляд на классическую дифференциальную геометрию
01:20:30
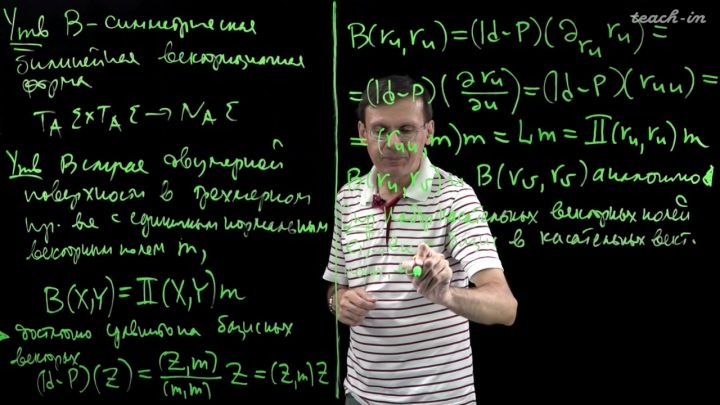
7
Лекция 7. Производная функции вдоль касательного векторного поля и производная векторного поля вдоль касательного векторного поля
01:15:48
8
Лекция 8. Символы Кристоффеля
01:30:29
9
Лекция 9. Тензор кривизны Римана
01:20:44
10
Лекция 10. Параллельный перенос и геодезические
01:18:41
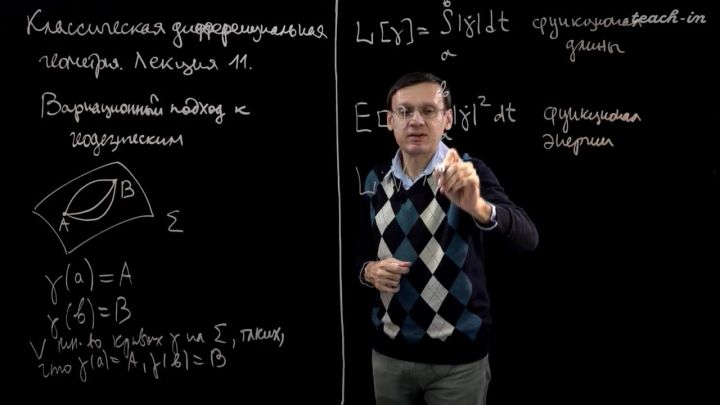
11
Лекция 11. Вариационный подход к геодезическим
01:16:03
12
Лекция 12. Продолжение обсуждения геодезических и параллельного переноса
01:25:37
13
Лекция 13. Следствие теоремы 12 лекции
01:04:43
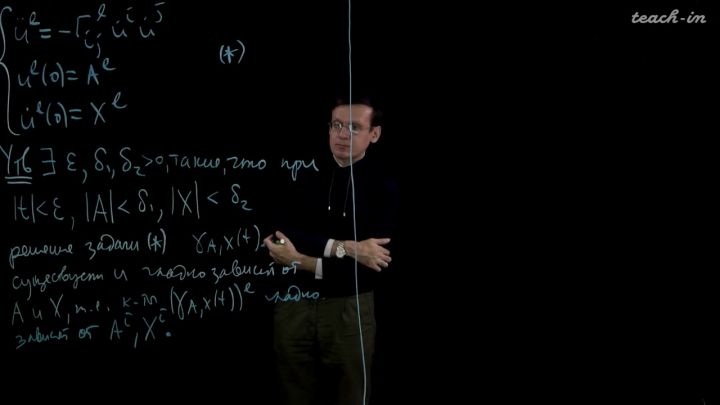
14
Лекция 14. Экспоненциальное отображение
01:13:32
15
Лекция 15. Минимальные поверхности. Поверхности постоянной (гауссовой) кривизны
01:05:53
16
Лекция 16. Теорема о поверхности постоянной гауссовой кривизны
01:21:21
Связанные курсы
15
Математика
Классическая дифференциальная геометрия
Иванов Александр Олегович
15
Математика
Классическая дифференциальная геометрия
Мохов Олег Иванович
16
Математика
Классическая дифференциальная геометрия
Дынников Иван Алексеевич
15
Математика
Классическая дифференциальная геометрия
Фоменко Анатолий Тимофеевич
21
Математика
Классическая дифференциальная геометрия
Шафаревич Андрей Игоревич