Лекции
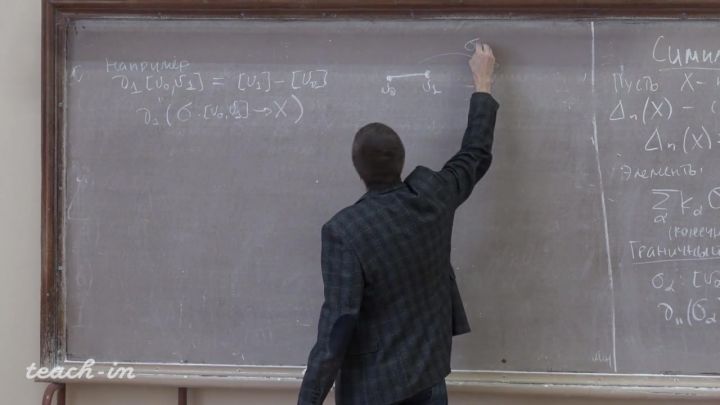
1
Лекция 1. Симплициальные гомологии
01:30:00

2
Лекция 2. Симплициальные гомологии (продолжение). Сингулярные гомологии
01:32:15
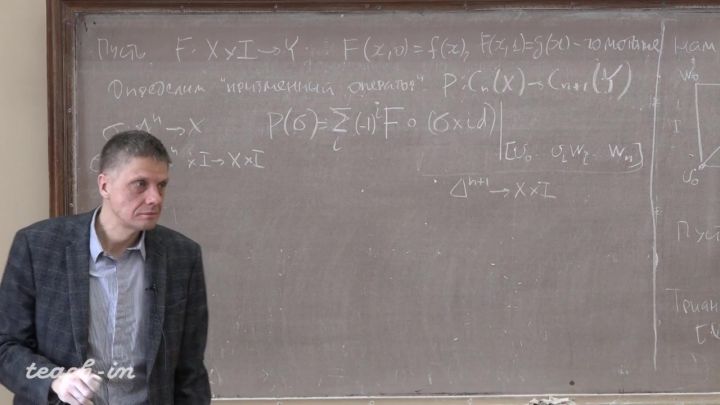
3
Лекция 3. Ключевые свойства сингулярных гомологий
01:26:45
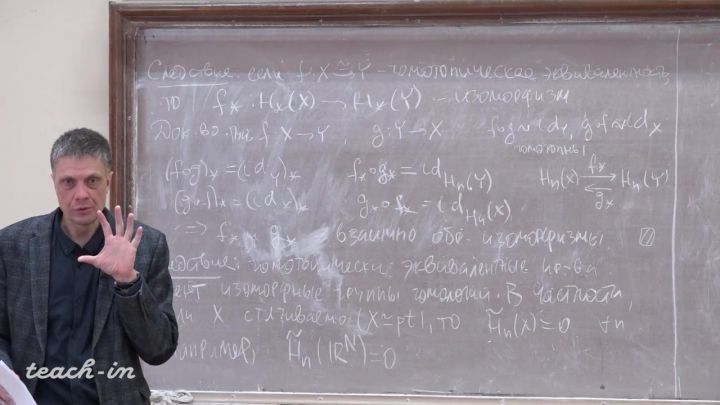
4
Лекция 4. Ключевые свойства сингулярных гомологий (продолжение)
01:28:16

5
Лекция 5. Теорема вырезания
01:25:58
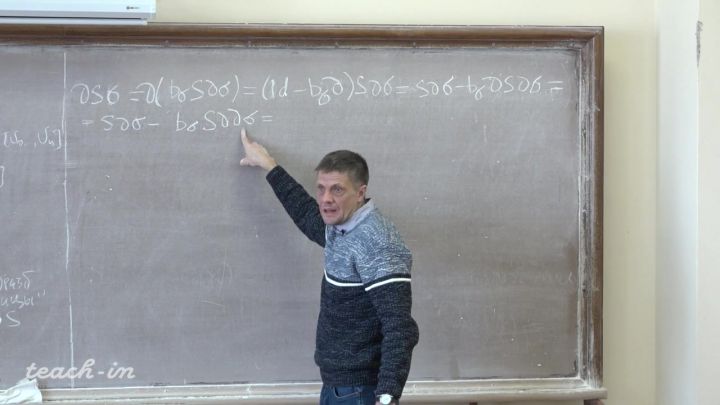
6
Лекция 6. Теорема вырезания (продолжение)
01:22:52
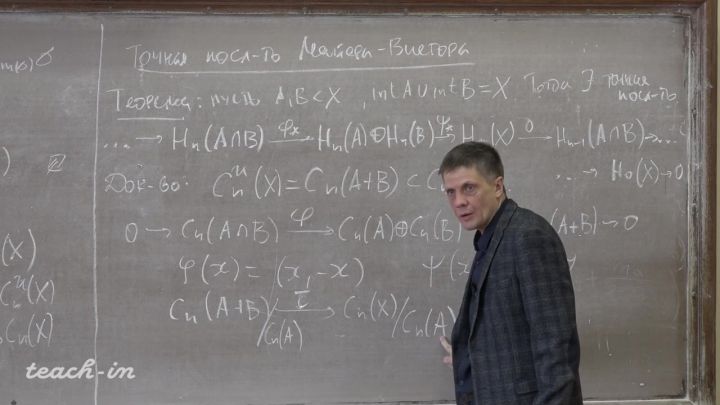
7
Лекция 7. Окончание первой части теории гомологий
01:28:22
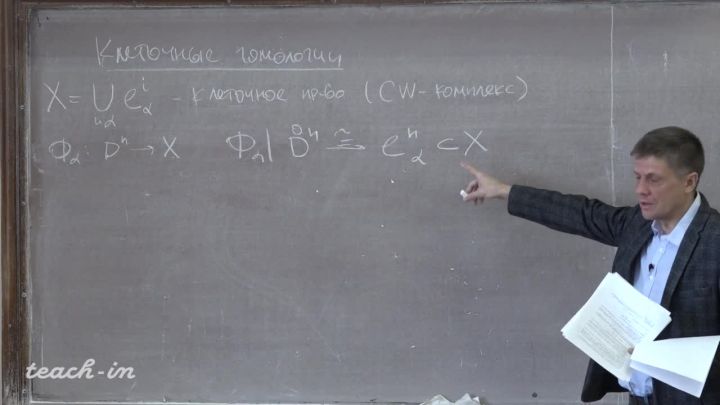
8
Лекция 8. Клеточные гомологии
01:30:48

9
Лекция 9. Клеточные гомологии. Связь с фундаментальной группой
01:30:04

10
Лекция 10. Гомологии с коэффициентами и когомологии
01:27:39

11
Лекция 11. Функторы Tor и Ext
01:28:43

12
Лекция 12. Кольцо когомологий
01:29:03

13
Лекция 13. Клеточное определение произведения пространств
01:25:07
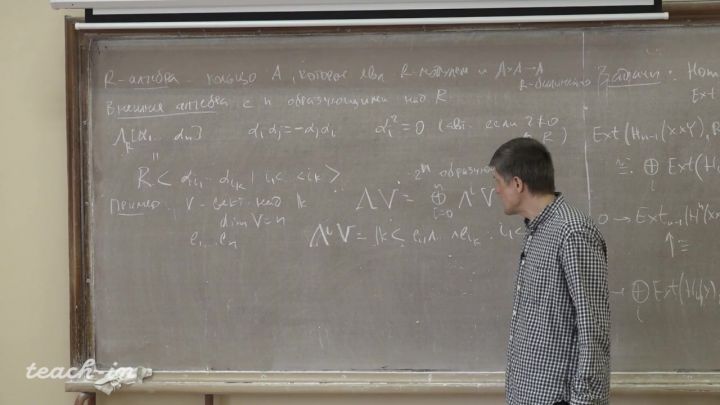
14
Лекция 14. Продолжение обсуждения формулы Кюннета и умножения в когомологиях
01:38:49
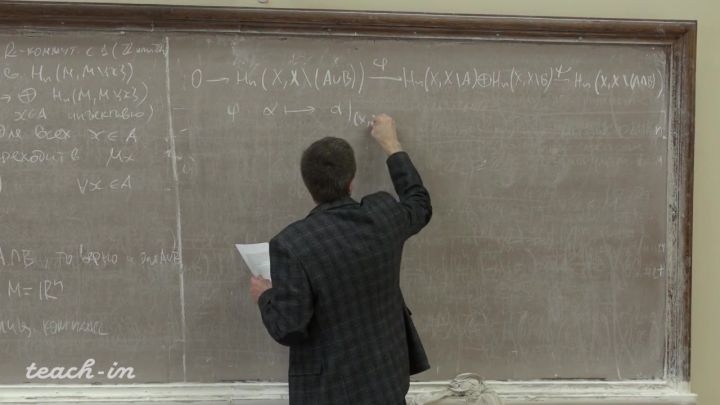
15
Лекция 15. Двойственность Пуанкаре
01:28:23

16
Лекция 16. Изоморфизм двойственности Пуанкаре
01:28:49
17
Лекция 17. Главная теорема по двойственности Пуанкаре
01:33:06

18
Лекция 18. Завершение обсуждения двойственности Пуанкаре
01:33:09
19
Лекция 19. Векторное расслоение
01:27:41

20
Лекция 20. Векторное расслоение (продолжение)
01:20:53

21
Лекция 21. Векторное расслоение (продолжение)
01:15:32

22
Лекция 22. N-мерные расслоения. Многообразие Грассмана
01:21:35
23
Лекция 23. Геометрия многообразий Грассмана. Клетки Шуберта
01:25:18

24
Лекция 24. Теорема Уитни. Класс Эйлера и класс Тома. Теорема Тома
01:29:07

25
Лекция 25. Ориентируемое векторное расслоение. Класс Тома и класс Эйлера
01:17:30

26
Лекция 26. Класс Эйлера и его свойства. Эйлерова характеристика и особые точки векторных полей
01:23:59
27
Лекция 27. Классы Понтрягина кватернионных и вещественных расслоений
01:31:38

28
Лекция 28. Точечная последовательность Гизина. Универсальные классы Понтрягина
01:28:43
