Лекции

1
Лекция 1. Интегральная сумма. Определенный интеграл Римана. Суммы Дарбу
01:29:18
2
Лекция 2. Свойства сумм Дарбу. Критерии интегрируемости. Интегрируемость непрерывных функций
01:33:27
3
Лекция 3. Классы интегрируемых функций. Основные свойства определенного интеграла
01:29:43
4
Лекция 4. Теоремы о среднем значении для определенного интеграла. Интеграл с переменным верхним пределом
01:39:35
5
Лекция 5. Замена переменной и интегрирование по частям. Несобственные интегралы первого рода
01:30:35

6
Лекция 6. Признак Дирихле. Абсолютная и условная сходимость. Несобственные интегралы второго рода
01:32:09

7
Лекция 7. Главное значение несобственного интеграла. Спрямляемые кривые и их длина
01:37:05
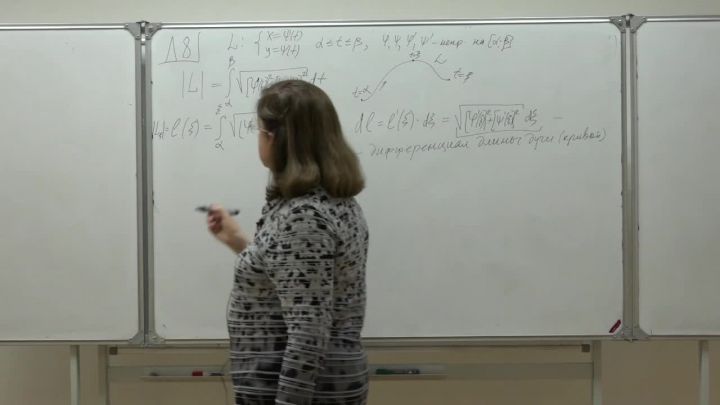
8
Лекция 8. Квадрируемые плоские фигуры и их площади
01:37:47

9
Лекция 9. Кубируемые пространственные тела и их объемы
01:33:18
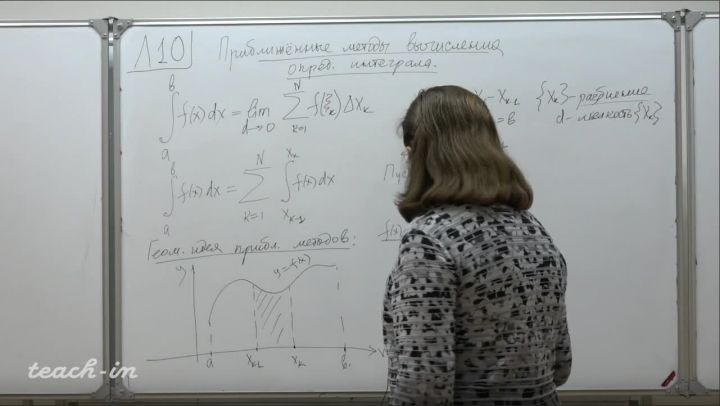
10
Лекция 10. Приближенные методы вычисления определенного интеграла. Методы хорд и касательных решения уравнений
01:54:03
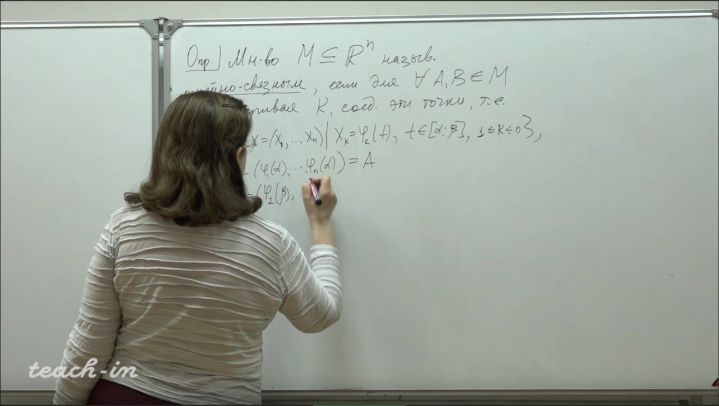
11
Лекция 11. Пространство R^n
01:39:28
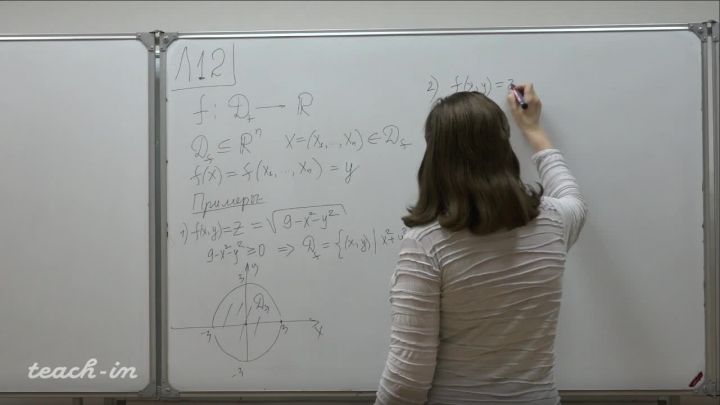
12
Лекция 12. Функции многих переменных. Предел и непрерывность функции многих переменных
01:26:57
13
Лекция 13. Локальные и глобальные свойства непрерывной функции нескольких переменных. Дифференцирование функции нескольких переменных
01:34:03

14
Лекция 14. Достаточные условия дифференцируемости функции нескольких переменных. Дифференциал и частные производные сложной функции
01:22:48
15
Лекция 15. Дифференцируемость сложной функции нескольких переменных. Градиент и производная по направлению. Частные производные и дифференциалы высших порядков
01:28:33
16
Лекция 16. Дифференциалы высших порядков. Формула Тейлора. Локальный экстремум функции нескольких переменных
01:32:28

17
Лекция 17. Квадратичные формы и их свойства. Достаточные условия существования локального экстремума функции нескольких переменных
01:30:14

18
Лекция 18. Неявные функции. Система неявных функций
01:34:46

19
Лекция 19. Условный локальный экстремум функции нескольких переменных. Метод неопределенных множителей Лагранжа
01:34:02

20
Лекция 20. Достаточные условия существования условного локального экстремума. Числовые ряды. Ряды с положительными членами
01:36:15

21
Лекция 21. Признаки сходимости рядов с положительными членами
01:30:48

22
Лекция 22. Знакопеременные ряды. Абсолютная и условная сходимость, теоремы Римана и Коши. Признак Дирихле-Абеля сходимости знакопеременных рядов
01:35:54
23
Лекция 23. Арифметические операции над сходящимися рядами. Бесконечные произведения и двойные ряды
01:39:11
