Лекции

1
Лекция 1. Гладкие регулярные кривые и поверхности в R^n, заданные параметрически или неявно
01:24:51
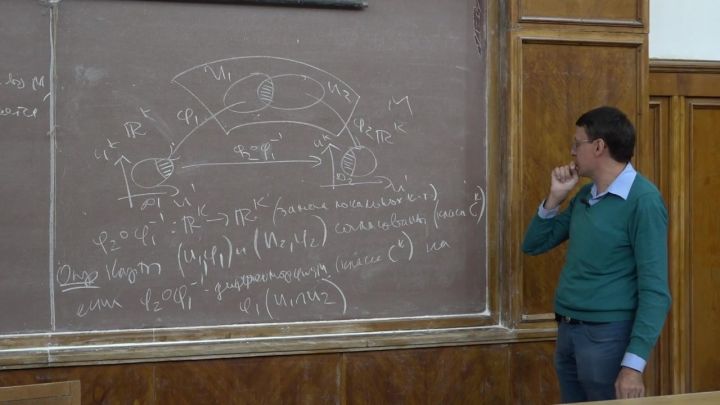
2
Лекция 2. Гладкие многообразия, гладкие функции
01:29:51
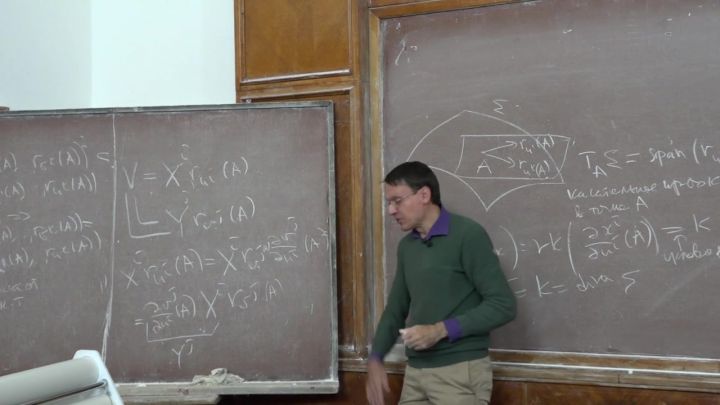
3
Лекция 3. Касательные векторы, производная вдоль вектора
01:35:16

4
Лекция 4. Векторные поля, коммутатор векторных полей
01:34:13

5
Лекция 5. Дифференциальные формы
01:26:02

6
Лекция 6. Дифференциальные формы. Алгебраические операции с дифференциальными формами
01:42:41

7
Лекция 7. Дифференциальные формы. Неалгебраические операции с дифференциальными формами
01:22:34

8
Лекция 8. Дифференциальные формы. Интегрирование дифференциальных форм
01:30:09

9
Лекция 9. Ориентация. Теорема Стокса
01:23:20

10
Лекция 10. Теорема Стокса. Разбиение единицы
01:30:12

11
Лекция 11. Римановы многообразия. Тензоры
01:28:05
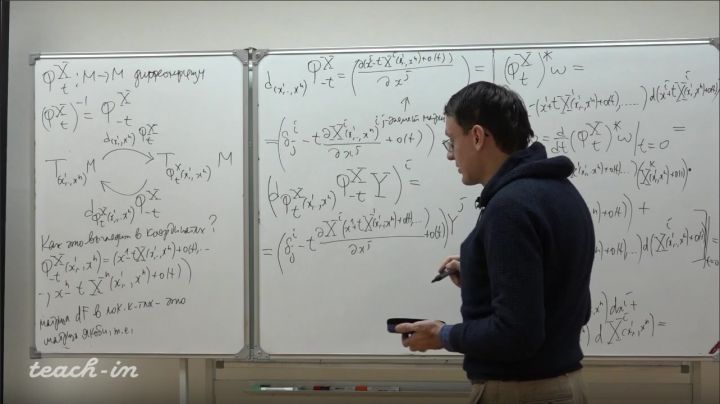
12
Лекция 12. Производная Ли тензорных полей. Подмногообразия
01:37:29

13
Лекция 13. Подмногообразия. Связности на многообразиях
01:32:12

14
Лекция 14. Связности. Параллельный перенос
01:18:13

15
Лекция 15. Геодезические
01:40:22

16
Лекция 16. Геодезические. Тензор кривизны Римана
01:15:49

17
Лекция 17. Когомологии де Рама
01:24:55
